F3 CIMA Exam Lab Questions

CAPM:

E(R)=Rf+β(Rm−Rf)E(R) = R_f + \beta (R_m - R_f)E(R)=Rf​+β(Rm​−Rf​)

Given:

E(R)=11%,Rf=2%,Rm=8%E(R) = 11\% , R_f = 2\%, R_m = 8\%E(R)=11%,Rf​=2%,Rm​=8%

0.11=0.02+β(0.08−0.02)⇒0.11−0.02=0.06β⇒0.09=0.06β⇒β=1.50.11 = 0.02 + \beta(0.08 - 0.02) \Rightarrow 0.11 - 0.02 = 0.06\beta \Rightarrow 0.09 = 0.06\beta \Rightarrow \beta = 1.50.11=0.02+β(0.08−0.02)⇒0.11−0.02=0.06β⇒0.09=0.06β⇒β=1.5

Beta > 1 ⇒ higher risk than the market.

PPA owns $500,000 of shares in Company ABB. Company ABB has a daily volatility of 2% of its share price

Calculate the 12-day value at risk that shows the most PPA can expect to lose during a 12-day period (PPA wishes to be 90% certain that the actual loss in any month will be less than your predicted figure)

Give your answer to the nearest thousand dollars.

A company has a 4% corporate bond in issue on which there are two loan covenants.

• Interest cover must not fall below 4 times

• Retained earnings for the year must not fall below S5 00 million

The Company has 100 million shares in issue. The most recent dividend per share was $0 10 The Company intends increasing dividends by 8% next year.

Financial projections tor next year are as follows:

Advise the Board of Directors which of the following will be the status of compliance with the loan covenants next year?

A company has:

   • A price/earnings (P/E) ratio of 10.

   • Earnings of $10 million.

   • A market equity value of $100 million.

The directors forecast that the company's P/E ratio will fall to 8 and earnings fall to $9 million.

Which of the following calculations gives the best estimate of new company equity value in $ million following such a change?

A)

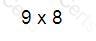
B)

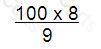
C)

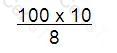
D)

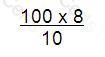
Option A

Option B

Option C

Option D