Databricks Related Exams
Databricks-Certified-Professional-Data-Scientist Exam







Refer to the exhibit.
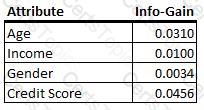
You are building a decision tree. In this exhibit, four variables are listed with their respective values of info-gain.
Based on this information, on which attribute would you expect the next split to be in the decision tree?
You have modeled the datasets with 5 independent variables called A,B,C,D and E having relationships which is not dependent each other, and also the variable A,B and C are continuous and variable D and E are discrete (mixed mode).
Now you have to compute the expected value of the variable let say A, then which of the following computation you will prefer